Harmonic Lattice Dynamics (handwriting notes)
July 29, 2020
Why the fuss
The harmonic lattice is a topic on my writing plan for quite some time. The Harmonic lattice approximation gives the birth of phonon, the starting point of the second quantization. Unlike my previous blogs, this one only shows some handwriting notes that I made during the past two days. For me, preparing these notes is a joyful journey. I discover new things that advance my understanding of the field theory and old things that I took for granted. Also, to my best knowledge, there is no fool-proof introduction to harmonic lattice dynamics in the context of quantum field theory. Physicists tend to make things over-complicated while skipping details crucial for understanding. Chemists give their full trust to physicists and borrow the derived formulae from solid-state textbooks directly. As an amateur physicist and half-chemist, I went through all the troubles to derive equations that finally lead to quantum field operators step by step. I believe I found a way to explain best the quantization of the harmonic lattice based on introductory quantum mechanics. The ending shows the most relevant results of the quantum field theory of phonons that provide creative tools for studying the condensed matter. A big reason for me to show handwriting this time is those bulky equations in my notes. I wish I can have more time to make new blogs like this because this old-school style challenges my resilience, both emotionally and intellectually. But new things have to wait until I finish my prelim exam.
One last thing, forgive my bad handwriting:).
Download PDF
You can find the binded PDF file here
PNG pages (11 pages in total)

Page 1

Page 2
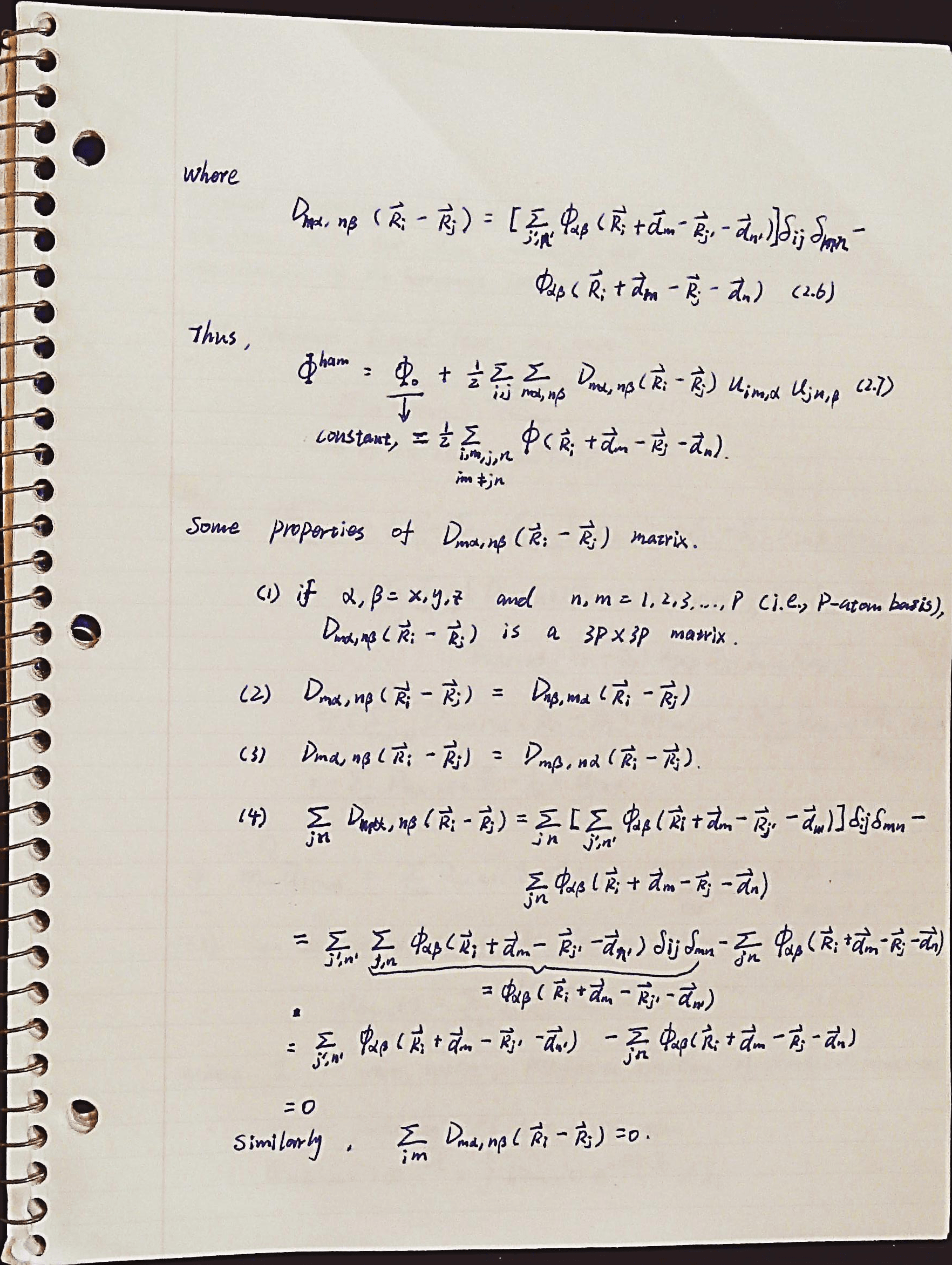
Page 3

Page 4

Page 5

Page 6
Page 7

Page 8

Page 9

Page 10

Page 11
Appendix: Several more words on Dynamic Matrix
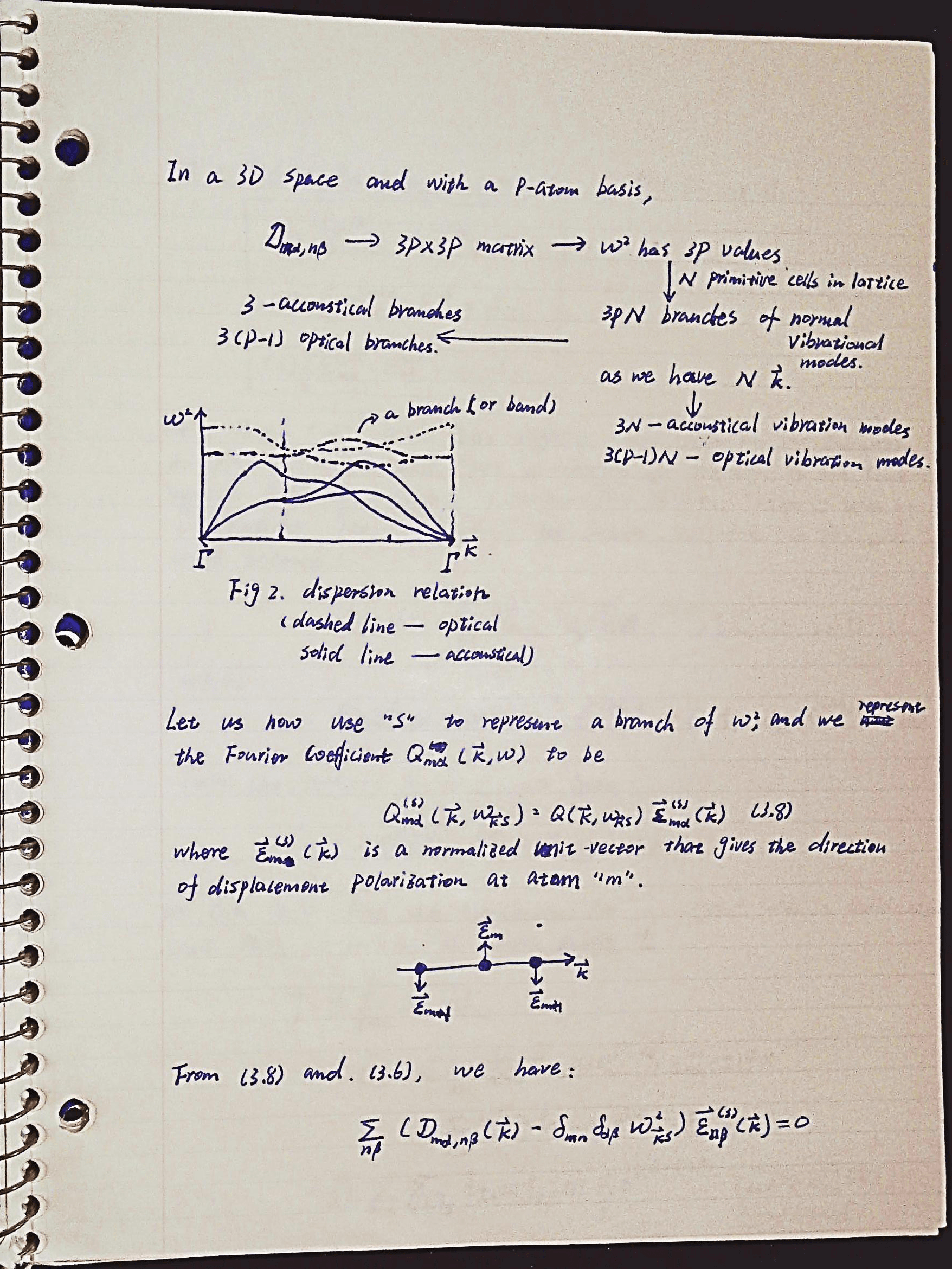
In the notes we already showed that the dynamic matrix \(\mathcal{D}_{m\alpha,n\beta}(\vec{\boldsymbol{k}})\) is the Fourier transform of another matrix \(D_{m\alpha,n\beta}(\vec{R}_i-\vec{R}_j)\), i.e.,
\[\mathcal{D}_{m\alpha,n\beta}=\sum_{\vec{R}_j}\frac{1}{\sqrt{m_mm_n}}D_{m\alpha,n\beta}(\vec{R}_i-\vec{R}_j)e^{-i\vec{\boldsymbol{k}}\cdot(\vec{R}_i-\vec{R}_j)}.\]Because the harmonic lattice energy can be represented using \(D_{m\alpha,n\beta}\) as,
\[\Phi^{ham}=\Phi^0+\frac{1}{2} \sum_{im\alpha,jn\beta}D_{m\alpha,n\beta}(\vec{R}_i-\vec{R}_j)u_{im,\alpha}u_{jn,\beta}\]the matrix \(D\) can also be calculated by
\[D_{i m \alpha, j n \beta}=\frac{\partial^{2} \Phi^{ham}}{\partial u_{im, \alpha} \partial u_{jn, \beta}}.\tag{A.1}\]We can easily calculate elements of matrix \(D\) using (A.1) if we know the explicit expression of \(\Phi^{ham}\) in terms of \(u_{im,\alpha}\).