Interesting Math Problems Solved Mechanically (keep updating)

July 14, 2020

Why

The youtuber 3Blue1Brown led me to Prof. Mark Levi’s Mathematical Mechanics, a collection of math problems solved by using mechanical intuitions. It is an eye-opening work, because I could never imagine that physics could be a perfect sevant for mathematics before. Solving problems using physics enpowers us to understand well-known theorems in an intuitive way, and the physical instinct embedded in the understanding really sheds lights in the ways of using the theorems efficiently. I will give my solutions to the exercise problems in the book here by transforming them into simple physical systems. Do not worry about too much Solving Hamiltonian in this blog, it is written in a more casual style comparing to my previous blog series, with the joy of problem solving being the primary focus.

From Curvilinear Triangle to Gas Tank

First we say it, formally…

Let me first state the original problem mathematically. Given a circle centered at point \(O\), we draw a tangent line at an arbitrary point \(T\) on the circle. We then choose a point \(A\) on the tangent line and shoot a laser line from \(A\) in a way that the laser intercepts with the circle at points \(P\) and \(Q\) (see the sketch below). Now, can you prove that \(AT^2=AP\cdot AQ\)?

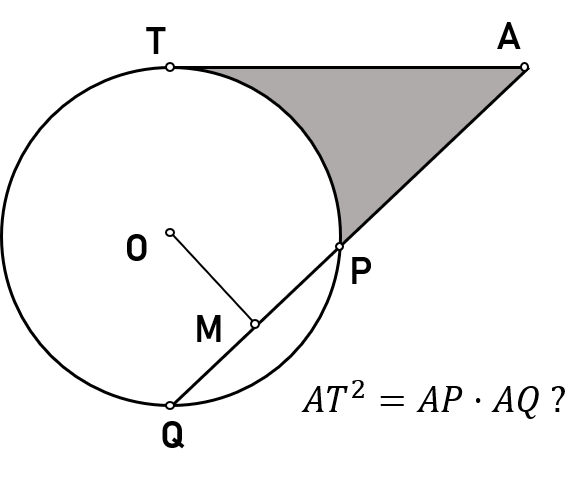
Figure 1. The sketch for our curvilinear triangle problem desribed above, where the point M is the middle point of the line segment PQ

Now we transform it, recklessly!

Imagine we have a gas tank with its shape being the shadow area in Figure 1 from a bird’s view. Next we allow the tank to only rotate around the point \(O\), the circle center, without any form of frictional forces applied to the tank. The height of the tank is irrelevant here because we assume no obstable to stop the movement if the tank is rotating. For people who know Newton’s theorems, we should conclude that the tank should remain still if we do not apply thrust force to it, i.e. the system is at its equilibirum state. The equilibrium condition indicates that the torques that the gas applied on the tank walls must be balanced.

We solved it, intuitively~

As we shall see now the torque balance leads to the proof of the statement in Figure 1. The shaded curvilinear triangle has one arc edge \(\overset{\frown}{PT}\) but luckily the torque applied by gas molecules bombarding the arc is zero. The reason for that is the force applied on \(\overset{\frown}{PT}\) pointing towards the circle point \(O\), which gives zero leverage distance. We now only consider the torques on the walls of \(AT\) and \(AP\), as shown in Figure 2.

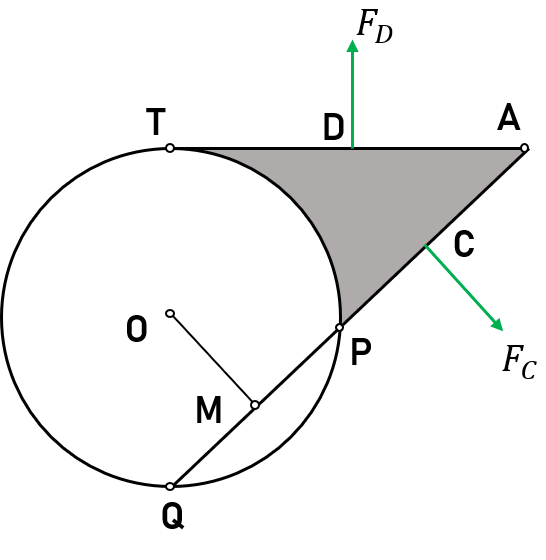
Figure 2. The sketch for transformed curvilinear triangle problem, where the forces applied on edges AT and AP are also labeled

According to the Pascal’s law the forces applied by the gas on the tank walls are uniformly distributed no matter how perculiar the shape of container is. So let us set the gas pressure on \(AT\) and \(AP\) to be 1 per unit length (we can always achieve this by changing the tank height, the irrelevant dimension of our problem). The forces on both walls can then be represented by the two forces \(F_D\) and \(F_C\) acting at the midpoints of \(D\) and \(C\), respectively. Using our newly defined pressure unit, it is obvious that \(F_D=AT\) and \(F_C=AP\). The torque applied by \(F_D\) is then

Notice that the leverage distance of \(F_C\) is \(MP+PC\), where \(M\) is the middle point of the chord \(PQ\), and

Because \(C\) and \(M\) are both midpoints, we immediately have

Thus the torque applied by \(F_C\) is

Using the torque balance \(q_C=q_D\), we finally get

Q.E.D.

A summary for now

The whole problem solving process is largely based on physical laws, i.e. Newton’s first law of motion and Pascal’s law, and yet the physics transformed the problem into a vivid picture of gas tank, and make the solution more creative. Math has been played the suportive role for every branch of science for so long, making people, even mathematician themselves forget that many math subjects started out with a physical problem in mind. Another Fields-metal-worthy example of physics serving math is the optimal transport theory.