A Graph-Theory Trick
August 1, 2020
Question
现有4支篮球队,A,B,C,D,打单循环赛。对每队来说,赢一场积3分,平一场积1分,输一场不得分。循环赛完毕后凭积分头两支队伍出线进入下一轮。那么一支队伍至少要积多少分才能确保一定出线?
A Simple Answer
这道问题实质上在问“一支队伍最高得多少分都有可能不出线?” 解决这个问题我们先找到一支队伍可能得到的分数,X。因为每支队伍要比3场,所以可能得到的分数为:
\[X=\{9,7,6,5,4,3,2,1,0\}\]很显然,当一支队伍得分是9分,那么该支队伍必须出线。如果一支队伍得到7分有没有可能不出线呢?答案是没有可能。得7分不出线的情况有两种:(1)有至少两支队伍得分超7分,或者(2)至少有三支队伍得分都是7分。我们现在证明这两种情况都不可能。假设队伍A 得到了7分,即A队两胜一平。我们子再假设A赢了B和C,平了D。那么A打完3局过后积分榜上得分应该是
| A | B | C | D |
|---|---|---|---|
| 7 | 0 | 0 | 1 |
在B,C,D 各剩下两场的情况下,这些队的最高分只有可能是7,即D 队积7分和A队一起出线。无论如何组合,当A,B,C,D其中一队得七分后,其他队不可能得分超过7,也不可能出现有3队同分的情况。因此,得7分队必出线。
我们接下来检验得6分有没有可能不出线。答案是有可能。我们再假设A队得6分,即赢两场输一场。我们再假设A被D打败了,那么A打完3局过后积分榜上的情况是:
| A | B | C | D |
|---|---|---|---|
| 6 | 0 | 0 | 3 |
接下来如果B打败了C和D,D又打赢了C,那么最终积分榜的情况是
| A | B | C | D |
|---|---|---|---|
| 6 | 6 | 0 | 6 |
即A,B,D三队同分。这种情况下没有队伍晋级。因此,一支队伍至少要得到7分才能确保一定出线。(解答完毕)
Generalized Answer
事实上,这是一道题隐含着图论(graph theory)的应用。单循环赛可以用图论中的锦标赛图表示。图中的每一个点代表一支队伍,每两个点用带箭头的边相连。比如上方最后一个表格所描述的情况在图论里表示为:
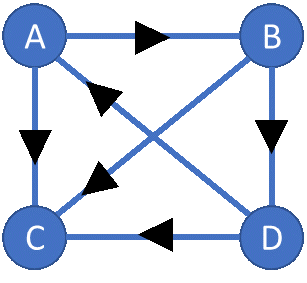
图 1.
上图中黑色三角的方向暗示比赛的输赢。比如链接 A 和 B 的边 AB, 其方向是由 A 到 B。说明 A 赢了与 B 的比赛。同时连接 A 和 D 的边 AD 是由 D 到 A,说明A 输掉了与 D 的比赛。图论中任意一点S向外相连的边称为它的外联边。 外联边的数量表示为 \(d^{+}(S),\) 反之称为内联边,其数量表示为 \(d^{-}(S) .\) 对于锦标赛图来说,我们很容易发现
\[d^{+}(S)+d^{-}(S)=n-1\tag{1}\]等式(1)中的n 代表图中点的数量。在图 1 中 \(n=4_{\circ}\) 如果我们定义“获胜数列”(win sequence)为
\[s^{+}=\left\{d^{+}\left(S_{1}\right), d^{+}\left(S_{2}\right), \ldots d^{+}\left(S_{n}\right)\right\}\tag{2}\]并且
\[d^{+}\left(S_{1}\right) \geq d^{+}\left(S_{2}\right) \geq \cdots \geq d^{+}\left(S_{n}\right)\tag{3}\]那么当n为偶数时。总有一个获胜数列为 \(s^{+}=\left\{\frac{n}{2}, \frac{n}{2}, \ldots, 0\right\}\tag{4}\)
当 n 为奇数时,总有一个获胜数列为
\(s^{+}=\left\{\frac{n-1}{2}, \frac{n-1}{2}, \ldots, \frac{n-1}{2}\right\}\tag{5}\) 如果 n 为偶数则至少要 \(\frac{3 n}{2}+1\) 分才能一定头两名晋级。当 n 为奇数时则需要 \(\frac{3 n-3}{2}+1\) 分才能确保晋级。